Spezial-Objektive
Kurze Brennweite (kürzer als normal): ringsum viel auf dem Bilde, da großer Bildwinkel, Darstellungsmaßstab klein = Weitwinkelobjektive·.
Lange Brennweite (länger als normal: ringsum weniger auf dem Bilde, kleiner Bildwinkel, Darstellungsmaßstab groß.
Will man sehr groß darstellen, so bekäme man gleichzeitig einen riesenhaften Auszug. Um das zu vermeiden, hat man sog. Tele-Objektive konstruiert. Sie bestehen aus einem normalen Objektiv, hinter das eine Zerstreuungslinse geschaltet worden ist. Die Zerstreuungslinse zieht das vom Objektiv erfaßte Bild noch etwas auseinander und bewirkt dadurch vergrößerte Darstellung ohne allzulangen Kamera-Auszug. Als Bildwinkel gilt dann der Winkel, den das Objektiv ohne Zerstreuungslinse erfaßt.
Das Einstellen eines Objektivs.
Bildweite - Gegenstandsweite
Wie ein Fernrohr oder einen Feldstecher kann man ein Objektiv auf bestimmte
Entfernungen scharf einstellen. Da das Einstellen einer Kamera schließlich
das A und O aller Fotografie ist, müssen wir hierauf etwas näher
eingehen.
| Einstellung | wie | bei | |||
|
|||||
| Fernsichten |
Das Objektiv ist auf seine Brennweite (auf Unendlich)
eingestellt. Diese Einstellung auf Brennweite zeichnet nur die Ferne
scharf, von einem gewissen Punkt an geht die Schärfe kilometerweit
hinaus (man nennt ihn den Unendlichkeitspunkt D).
| Einstellung | wie | bei | figürlichen | Szenen | |
|
|||||
| usw. |
Das Objektiv ist auf ein näheres Objekt eingestellt.
Dann heißt die Entfernung Objektiv - Mattscheibe (Platte, Film)
Bildweite. Bei Naheinstellung wird auch der Darstellungsmaßstab
größer.
* ) Bildwinkel 80 bis über 1000
Seite 162
zur
Inhaltsübersicht![]() zum
Stichwortverzeichnis
zum
Stichwortverzeichnis
| Einstellung wie bei Porträts usw. |  |
Die Bildweite wächst, wenn auf noch nähere
Entfernung eingestellt wird. Auch der Darstellungsmaßstab wächst.
| Einstellung wie bei Aufnahmen in natürlicher Größe | 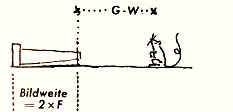 |
Hat die Bildweite die Länge von 2mal Brennweite,
so wird ein Gegenstand in natürlicher Größe dargestellt.
Auch die Gegenstandsweite (Objektiv-Objekt) muß hierbei die Größe
von 2mal Brennweite haben. Dieses Gesetz gilt für jede beliebige
Brennweite.
Die Bildweite ist von großer praktischer Bedeutung. Je länger
sie wird, desto mehr verschlechtert sich das Öffnungsverhältnis
(S. 165).
Ein einfaches Beispiel: durch ein Fenster
von bestimmter Größe wird ein kleines Zimmer besser ausgeleuchtet
als eine Kegelbahn. Der Kegelbahn entspricht der lange Auszug (die Bildweite)
bei Naheinstellung. Der Lichtabfall bei Auszugsverlängerung wächst
sofort rapid, nämlich im Quadrat. Deshalb erfordert auch doppelter
Auszug vierfache Verlängerung der Belichtungszeit. Schon bei Einstellung
auf sehr nahe Objekte wird der Kamera-Auszug relativ lang (je länger
die Brennweite, desto länger wird er faktisch und relativ zur Brennweite).
Deshalb sollen Nahaufnahmen grundsätzlich etwas reichlicher belichtet
werden. Die Belichtungszeit für sehr lange Auszüge berechnet
man nach folgender Formel:
(Bildweite ) ²
(Brennweite )![]() mal Belichtungszeit.
mal Belichtungszeit.
Als Faustregel kann man sich merken:
| Auszug (Bildweite) | = 1 ½ x Brennweite | = 2)fache Verlängerung |
| Auszug (Bildweite) | = 1 ¾ x " | = 3) der Belichtungszeit |
| Auszug (Bildweite) | = 2 x " | = 4) |
Seite 163
zur
Inhaltsübersicht![]() zum
Stichwortverzeichnis
zum
Stichwortverzeichnis
 |
Seban Reiserer † Erntedankfest 24/36 mm F 5 cm
Isopan FF
Einige Formeln
Die Beziehungen zwischen Brennweite, Bildweite und Gegenstandsweite
sind durch die sog. "Linsenformel" festgelegt. Sie lautet:
|
1
|
1
|
1
|
||
| Gegenstandsweite | + | Bildweite | = | Brennweite |
Je nachdem, welche der drei Größen ermittelt werden soll,
ergeben sich dann (wenn die beiden anderen Größen bekannt
sind) folgende Rechnungen:
 |
Auch den Abbildungsmaßstab kann man,
sofern Bildweite und Gegenstandsweite bekannt sind, folgendermaßen
errechnen:
Bildweite
Gegenstandsweite
Auf Grund der Mattscheiben-Kontrolle ergibt sich der Abbildungsmaßstab
natürlich viel schneller, indem man Abbildungsgröße
und Gegenstandsgröße zu einander in Beziehung setzt.
Seite 164
zur
Inhaltsübersicht![]() zum
Stichwortverzeichnis
zum
Stichwortverzeichnis
Lichtstärke - relative Öffnung - wirksame
Öffnung
Lichtstärke und relative Öffnung (auch "Öffnungsverhältnis")
sind im Sprachgebrauch identische Begriffe. Sie besagen, daß sich
Objektivdurchmesser und Brennweite in dem und dem Verhältnis zu
einander befinden. Der Durchmesser des Objektivs allein sagt nichts
über die Lichtstärke aus. Um unser Beispiel von vorhin wieder
heranzuziehen: man muß wissen, ob ein Fenster von bestimmter Größe
ein kleines Zimmer oder eine Kegelbahn ausleuchten soll. Entscheidend
ist also die Entfernung der Rückwand. Die Rückwand ist aber
in unserem Fall die Mattscheibe (Platte, Film). Und diese Entfernung
wird durch die Brennweite bestimmt. Also muß man den Durchmesser
des Objektivs zur Brennweite in Beziehung bringen, um die Lichtstärke
zu erfahren (daher ja auch relative Öffnung, Öffnungsverhältnis).
Wenn ein Objektiv die relative Öffnung 1 : 4 hat, so besagt das,
daß sich der Objektiv-Durchmesser zur Brennweite verhält
wie 1 : 4.
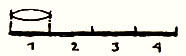 |
Ganz korrekt ist das nicht, denn nicht den freien Objektivdurchmesser
setzt man in Beziehung zur Brennweite, sondern die sog. wirksame Öffnung.
Zwar genügt es in der Praxis, den freien Durchmesser zu benützen,
denn die wirksame Öffnung ist stets nur um eine Kleinigkeit größer.
Aber auch sie kann stets leicht ermittelt werden: steht auf einem Objektiv
z. B. 1 : 4,5 F = 10 cm, so ergibt sich die wirksame Öffnung aus
dem Divisionsexempel 10 _ 4,5. Die wirksame Öffnung beträgt
in diesem Falle 2,2 cm.
Man kann die wirksame Öffnung auch experimentell ermitteln: man
stellt die Kamera im Zimmer auf, die geöffnete Rückwand in
Richtung auf ein Fenster. An die Objektivfassung drückt man eine
Mattscheibe. Der helle Kreis, der sich auf der Mattscheibe abbildet,
ist die wirksame Öffnung.
Niemals miteinander zu verwechseln sind also. relative Öffnung
(= Öffnungsverhältnis = Lichtstärke), freie Öffnung
(= Durchmesser der Objektiv-Öffnung in cm) und wirksame Öffnung;
(= Brennweite : Lichtstärkenzahl).
Komplizierter Fall bei einer Nah-Aufnahme
Jemand will einen kleinen Gegenstand mit der 9/12-Kamera recht groß
aufnehmen. Dann sagt er sich: wenn ich meine Brennweite durch eine Vorsatzlinse
verkürze, werte ich den Auszug meiner Kamera am besten aus, er
wird dann (relativ zu der verkürzten Brennweite) lang. Denn jede,
auch die kürzeste Brennweite, folgt dem Gesetz von S.
163, daß ein Auszug von der Länge zweier Brennweiten
Darstellung in natürlicher Größe ergibt (über Darstellung
in mehr als natürlicher Größe s.
S. 177). Das ist übrigends der Grund, weshalb man die
kleindarstellenden kurzen Brennweiten für großdarstellende
Nahaufnahmen verwendet, - sie sparen Auszugslänge.
Seite 165
zur
Inhaltsübersicht![]() zum
Stichwortverzeichnis
zum
Stichwortverzeichnis
Rechnerisch liegt dieser
Fall aber nicht so einfach. Es ist nicht ganz unkompliziert und zum
mindesten langwierig, die Belichtungszeit umzurechnen auf Grund folgender
drei Tatsachen: erstens, da DIE VERKÜRZENDE Vorsatzlinse zunächst
einmal das ursprüngliche Öffnungsverhältnis des Objektivs
verändert hat (in diesem Fall verbessert), zweitens, daß
die neue verkürzte Brennweite mit sehr langem Auszug (sehr großer
Bildweite) verwendet wird. (Diese Rechnung allein wäre zwar nach
S.
163 leicht.) Aber es kommt drittens noch die Blendung
zum Zwecke der Tiefenschärfe hinzu. Darüber hinaus muß
man viertens meist feststellen, daß man nun eigentlich nicht weiß,
welcher Blendenzahl die zur Aufnahme gewählte Blende entspricht,
denn die auf dem Objektiv eingravierten Blenden stimmen natürlich
für die verkürzte Brennweite nicht.
Das alles läßt sich, wie gesagt, ausrechnen. Aber man durchschneidet
diesen Knoten mit einem Schlage, wenn man folgendermaßen verfährt:
Man führt das ganz schlichte Rechenexempel
Auszuglänge
wirksame Öffnung durch.
Es ist das gleiche Exempel, mit dem bei jedem Objektiv das Öffnungsverhältnis
(die Lichtstärke für Unendlich-Auszug) schon vom Fabrikanten
ermittelt wird.
Wie man die wirksame Öffnung experimentell ermittelt, wurde weiter
oben auf S. 165
gesagt. Dann stellt sich auch dieser komplizierte Fall sehr einfach
dar. Nehmen wir an, der Auszug (die Bildweite) wäre 25 cm lang
und das stark geblendete Objektiv hätte eine wirksame Öffnung
von 0,5 cm, so hätte man damit eine relative Öffnung eine
Blende von ![]()
Zur Not und ohne einen entscheidenden Rechenfehler zu
begehen, könnte man auch den freien Durchmesser des Objektivs als
Divisor nehmen, indem man ihn ein wenig reichlicher einsetzt.
Über einen kleinen Einstelltrick bei der Aufnahme lebender, sehr
kleiner Objekte siehe unter ABC
Seite 218.
Seite 166
zur
Inhaltsübersicht![]() zum
Stichwortverzeichnis
zum
Stichwortverzeichnis
Der Lichtverlust im Objektiv
Zwar ist es allgemein Sprachgebrauch, aber nicht ganz korrekt, wenn
man relative Öffnung und Lichtstärke identisch setzt. Kein
Objektiv hat die Lichtstärke, die es theoretisch haben müßte.
Je höher nämlich die Anzahl der Linsen, aus denen das Objektiv
besteht, desto größer der Lichtverlust durch Absorption im
Glase und durch Reflexion auf den spiegelnden Flächen. Aus Untersuchen
von A. Klughardt seien folgende Beispiele genannt.
Man sieht, daß im allgemeinen mit der Zahl der Linsen der Lichtverlust
wächst, und daß man sich dann um so weiter von der theoretischen
Lichtstärke entfernt. Die praktische Konsequenz, die man aus diesen
Tatsachen ziehen muß, kann lediglich die sein, daß man den
bei 3,5 und 4,5 vorliegenden Lichtverlust als normal und unabänderlich
betrachtet, sich aber sagt, daß viellinsige lichtstarke Objektive
einen zusätzlichen Lichtverlust zeigen, der dann schon recht erheblich
ist. Eine besondere Rolle spielt neben der Anzahl der Linsen die Menge
der gegen Luft stehenden spiegelnden Flächen. Will man den ungefähren
Lichtverlust eines bestimmten Objektivs wissen, so informiert man sich
über seine Konstruktion und kann dann mit Hilfe der obigen Tabelle
annähernd auf den Lichtverlust schließen.
Wie rechnet man Blenden um?
Belichtungsmesser und -tabellen erübrigen das Rechnen. Es kann
aber geschehen, daß man schnell einmal eine Rechnung im Kopf vornehmen
muß. Das ist mit Hilfe einer Faustregel sehr einfach. Man verfährt
stets so:
Große Blendenzahl
kleine Blendenzahl
Das Ergebnis mit sich selbst multipliziert (ins Quadrat erhoben) ergibt
dann den Faktor für die Verlängerung oder Verkürzung
der Belichtungszeit. Ein Beispiel: man will von der Blende 3,5 auf die
kleine Blende 18 übergehen und wissen, um das wievielfache dies
die Belichtungszeit verlängert. Dann große Zahl durch kleine,
in diesem Fall 18 : 3,5 =rd. 5. Diese 5 mit sich selbst multipliziert
= 25. Für Blende 18 ist also 25mal so lange zu belichten wie für
Blende 3,5. Geht man umgekehrt von der kleinen Blende auf die große
über, also etwa von 18 auf 3,5, so bleibt die Rechnung die gleiche.
Nur daß in diesem Fall die Belichtungszeit den 25. Teil der für
Blende 18 beträgt.
Bei dieser Gelegenheit sei noch erwähnt, daß die genaue Folge
der deutschen Blendenreihe die ist:
18 - 12,5 - 6,3 - 4,5 - 3,2 - 2,2 - 1,6. Dann erfordert jede größere
Öffnung die halbe Belichtungszeit der vorhergehenden. Nach dem
internationalen Blendensystem (Zeiss) heißt die Folge: 16 - 11
- 8 - 5,6 - 4 - 2,8 - 2 - 1,4.
Seite 167
zur
Inhaltsübersicht![]() zum
Stichwortverzeichnis
zum
Stichwortverzeichnis![]() weiter
weiter

